Say we start with one cell, put it in minimal medium, where it and its daughter cells will grow and divide once every hour:

In minimal medium , E. coli divides typically in 60 min., or 1 generation= 60 min.

We can calculate how long it will take to get a billion cells from just one:

Let g = number of generations. 2 gens. --> 4 cells, 3 gens. --> 8 cells, or N (no. of cells) =1 x 2^g (starting with one cell).
If we started with 100 cells, after 1 gen. we would have 200 and after 2 gens. 400, 3 gens., 800 etc.

More generally, starting with N_o cells: N = N_o x 2^g

Since we want to know how much time it will take: express generations in terms of time.
If we let t_D = the generation time, or doubling time, then the number of generations that have passed during the time interval t is just t/t_D: So g = t/t_D.
So now N = N_o x 2^t/tD. One can thus see that growth is exponential with respect to time.

Now we could solve this equation for t, since we know we want N to be 1 billion, N_o is 1, and t_D is 1 hr. Taking the logarithm base 2 of both sides:

log₂ (N/N_o) = t/t_D, or t = t_Dlog₂(N/N_o) = 1 X log₂ (1,000,000,000/1) = log₂(10⁹)

But suppose your calculator doesn't do log base 2.  No problem, convert to log base 10 ("log") or natural log base e ("ln").

log₂X = logX/log2 = logX/0.3 and log₂X = ln_eX/ln_e2 = lnX/0.69 (Also: 2^x = 10^xlog2 and 2^x = e^xln2)

So log₂(N/N_o) = log(N/N_o)/log2 = t/t_D  or log(N/N_o) = (log2/t_D)t = Kt, where K=log2/t_D or K=0.3/t_D.

Or back to the exponential form: N/N_o =10^Kt or: N =N_o10^Kt

Or, since most scientific calculators have natural log functions:

N = N_oe^Kt, where K = ln2/t_D = 0.69/t_D, another common form of the exponential growth equation.

We could also have approached this question of rates of change of N with time more naturally using calculus (Note: familiarity with calculus is not necessary for this course.)  If you have a million cells, then after one generation time you’ll have gained 1 million. If you had 100, you would’ve gained 100. In general, the rate of increase of N with time is just proportional to the number of cells you have at any moment in time, or: dN/dt = KN

Separating variables: dN/N = Kdt.
Integrating between time zero when N = N_o and time t, when N = N:

lnN - ln N_o = Kt - 0, or ln(N/N_o) = Kt, or N = N_oe^Kt

We can calculate the constant K by considering the time interval over which N_o has doubled. This time is the doubling time, t_D. For that condition:
N/N_o = 2 = e^KtD. Taking the natural logarithm of both sides: ln2=Kt_D, or K=ln2/t_D, exactly as above.

In summary:

All this looks worse than it is. Exponential growth using a base of 2 is intuitively obvious.  And once you see the derivation, the exponential growth equation using log or ln can be simply applied to problems using a calculator.  You just have to keep track of what you know and what you are after. 

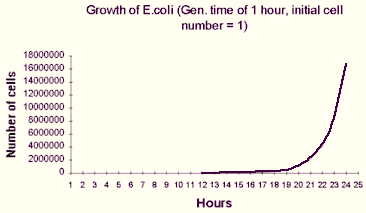
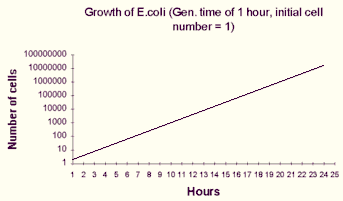
Graphically, the depiction of exponential growth looks  like this:	Or, with the ordinate (Y-axis) plotted on a logarithmic scale, a semi-log plot:

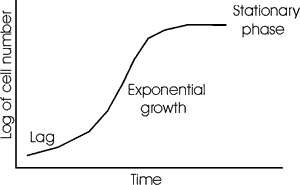
In reality, there's a lag before cells get going, and there's a limit (thankfully) to cell density, as nutrients become exhausted and/or toxic excretions accumulate.  The final plateau is called stationary phase:

© Copyright 2000  Lawrence Chasin and Deborah Mowshowitz   Department of Biological Sciences   Columbia University   New York, NY