lec7_01.html

Biology C2005 Lecture 7

::Enzyme specificity::
Proteins act as catalysts in a way similar to that described for platinum last time; they providing a surface that facilitates the formation of a transition state complex for the reactants by bringing together the reactants (or substrates as the reactants that bind to such a protein are called). They also often influence the bonds in the substrates to facilitate the formation of new bonds. THEY DO NOT INFLUENCE THE DIRECTION OF THE REACTION, ONLY THE RATE. (Look back at the energy diagram: one cannot reverse the thermodynamic facts of life, the direction of the reaction is determined by the relative energy levels of the reactants and products in the diagram). Such biological catalysts are called enzymes. Most enzymes are proteins, and a large fraction of proteins are enzymes. But RNA, a nucleic acid, can also act as an enzyme catalyst, although so far few such reactions have been identified. The surface pocket in the enzyme where the chemical transformation of the substrates takes place is called the ACTIVE SITE of the enzyme. See picture, and [Purves6ed 6.15a].
Unlike the Pt catalysts, which can bind many different kinds of molecules, protein surfaces can act with great specificity with respect to their substrates, being tailored to the charge, the shape, and/or the hydrophobicity of the substrates. See [Purves6ed 6.13]. The surface pocket provides the specificity:

(Remember the ala and gly binding protein models surfaces we just discussed as simplified models of how such specificity can be achieved...)

For example, Pt will also catalyze the hydrogenation of C=C double bonds. It will do this for any C=C bond, including those double bonds we first met in the description of unsaturated fatty acids, making peanut butter or margarine. Whatever fat you try, works.

::Substrates & products::
But consider an enzyme, let's say the enzyme succinic dehydrogenase that catalyzes the hydrogenation of the unsaturated dicarboxylic acid fumaric acid (or fumarate, for short) [are you getting all these terms?]

                                            succinic dehydrogenase
HOOC-HC=CH-COOH ---------------------------------------> HOOC-CH₂-CH₂-COOH
                                                        + 2H
fumaric acid                                                                              succinic acid

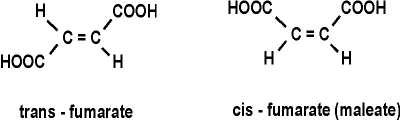
Note the enzyme name, an indication that enzymes do not alter the direction of the reaction: here it is named for the reverse reaction (a dehydrogenation), which it also catalyzes. Compounds that are NOT substrates for this enzyme include:

1-hydroxy-butenoate:    HO-CH=CH-COOH (OH instead of one of the carboxyls)

cis-fumarate (called maleate):

maleic acid: HOOC-CH=CH-COOH (H's on the central C's here are cis (on the same side of the C=C double bond); in fumarate the H's are trans (on opposite sides of the C=C double bond):

Thus the 3-D structures of the small molecules, as well as of the proteins, are critical. They must be the right shape to fit. So unlike chemical catalysts, enzymes are highly specific about the reactions they catalyze because they are highly specific about the substrates they bind. See animation - pause lecture audio before viewing this movie - (This is a 4 MB download, worth it only if you can do something else useful while fetching it or are connected directly to the CU network).

In summary, enzymes bind SUBSTRATES with great specificity, and they lower the activation energy for the chemical reaction that converts these substrates into PRODUCTS, thus greatly speeding up these reactions. It is the 3-dimensional shape of the pockets, usually at the surface of the proteins, that provides this specificity.

The texts give several examples of how specific enzymes act as catalysts.

So enzymes are catalysts, and catalysts speed up chemical reactions. To characterize the function of enzymes as catalysts, to analyze this speeding up in more detail, let's now consider the rate of chemical reactions (or chemical kinetics) in more quantitative terms.

::Chemical kinetics::
For the general reaction of substrate --> product, or S --> P, the velocity of the reaction is the appearance of product per unit time, or the change in concentration of the product per unit time, or:

V = delta[P]/delta[t], or d[P]/dt.

And, if V = d[P]/dt, then V must also = -d[S]/dt, or the rate of disappearance of substrate per unit time.

And, from the laws of mass action: V = k₁[S] - k₂[P]

That is, the rate of the forward reaction is proportional to the concentration of substrate and the rate of the back reaction is proportional to the concentration of product, and the net rate forward is the algebraic sum of these two processes. The rate constants, the k's are here by definition. To simplify the situation, and to simulate a common laboratory case, let's consider just an initial condition, with all S but no P around yet. Under these conditions [P] is so small the back reaction (P --> S) can be ignored. We will always only be considering this simplified case in our discussion of enzyme kinetics. So:

Vo = k₁[S]

where Vo indicates an INITIAL VELOCITY, before P builds up to the point where the back reaction becomes significant. (Understand: I may drop the naught sign and just say V, but I always mean the initial velocity in the following arguments.)

If we plot P vs. t, we get a straight line.

However, the rate of the reaction, which is the slope of this line, will be proportional to the first power of [S]. (It is called a first-order reaction.) If we consider a series of reactions, each starting with a different amount of S, we would get a series of straight lines with different slopes:

Now let's consider the dependence of the initial reaction RATE on the concentration of the reactant or substrate S:

Imagine a series of test tubes with different increasing concentrations of S, and measure P vs. t slopes for each one .

Now plot that slope (which is Vo) for each different initial S's, i.e., Vo vs. [S]. we again get a straight line, characteristic of a first order reaction.

This was the reaction rate with the pure chemicals. Now let's repeat the experiment but add a pinch of enzyme that catalyzes this reaction. Same amount to each test tube.

First of all, the rate is greatly increased.

The difference is so great that we can ignore the uncatalyzed chemical reaction as being insignificant compared to the enzyme catalyzed reaction [Purves6ed 6.16].

Now a plot of Vo vs. [S] looks a little different, for the enzyme-catalyzed reaction:

We can talk about two parts to this curve, the beginning, at low S, where Vo is proportional to S, the reaction being first order.

And the end, where V is independent of S, the reaction being zero order.

::Michaelis - Menten equation::
Michaelis and Menten formulated this situation mathematically in 1913, with some simplifying assumptions that turn out to be OK for most cases.

The first assumption is that an enzyme-catalyzed reaction proceeds through an intermediate, called the enzyme-substrate complex, as follows:

First, enzyme (E) and substrate (S) interact to form an enzyme-substrate complex (ES). Second this ES complex either dissociates back to E and S, or the substrate undergoes a transformation to the product, P, which then dissociates from the complex. Each step is characterized by a first order rate constant, called k1 through k4. The numbering is important here, to allow us to talk about these individual steps.

This model can explain the observed way in which the velocity of an enzyme-catalyzed reaction depends on the substrate concentration (redrawing the curve from last time):

With 3 assumptions we can derive an equation that relates velocity to substrate concentration, the Michaelis - Menten equation:

Assumption 1. E + S <--> ES: this is how enzymes work, via a complex
Assumption 2. Reaction 4 is negligible, when considering INITIAL velocities
Assumption 3. The ES complex is in a steady-state, with its concentration unchanged with time during this period of initial rates. Steady state is not an equilibrium condition, it means that a compound is being destroyed at the same rate as it is being formed, so that its concentration remains constant.

That is, the ES complex is being formed by reaction k1 as fast as it is being disassembled by reactions k2 and k3, so its concentration (the concentration of ES) is not changing. It quickly reaches this steady state by the laws of mass action. See the handout on enzyme kinetics to follow the mathematical consequences of this assumption.

::Vo, Vmax, K_m, turnover number::
The enzyme kinetics handout shows then how by applying the chemical kinetic principle of rate constants and straightforward algebra, you get the following formula relating the initial velocity of an enzyme-catalyzed reaction to the substrate concentration:

Vo= k3[E^o][S] /[(k2+k3)/k1] +[S]

     where E^o = the initial, or total, enzyme concentration and [S] (with or without the brackets) is the substrate concentration, assuming here the simple case of one substrate.

We can simplify this equation by substituting one constant, K_m (the Michaelis constant), for the group of 3 rate constants in the denominator, so:

Vo= k3[E^o][S] where K_m=k2+k3
         K_m + S                     k1

Here, again:
E^o is the total concentration of enzyme (free and bound in the complex),
K_m is the Michaelis constant,
S is the substrate concentration
k3 is the rate constant for the formation of P from ES, which you should verify from the diagram of the reaction mechanism.

Looking at the equation we can see:

1- that the rate of the reaction is proportional to the enzyme concentration. This is reasonable, since the enzyme is the necessary catalyst, and is almost always a rate-limiting factor.
2- that for a given amount of enzyme, S determines the rate of the reaction, as all other factors are constants.
3- now at low S, i.e., how low? low compared to K_m, where S << K_m, the denominator approaches K_m, and the rate is simply proportional to S, as is observed.
4- On the other hand, at high S, i.e., where S >> K_m, the denominator approaches {s}, and the [S]'s cancel out from numerator and denominator, so the rate is independent of [S], and V simply = k3E^o, also fitting the observed shape of the experimental curve.

Now let's bring these constants, K_m and k3, to life; they have some particular significance for describing an enzyme. Let's review for a minute just what an enzyme does:

1. It catalyzes the chemical transformation of substrate into product, helping to break targeted covalent bonds in the substrate.

2. It display exquisite specificity in doing so, being able to bind one substrate but not another of very related structure.

The constants that reside in the Michaelis-Menten equation relate to these two properties of enzymes as follows:

Consider k3: At high S, V approaches a maximum for a given amount of enzyme, called Vmax.

So: Vmax = k3E^o, the rate at high [S].

When Vmax is reached, all of the enzyme E exists as ES; it is saturated, it is turning S into P as fast as it can. Now we can once again re-write the Michaelis-Menten equation in an even more simplified form:

V = Vmax[S]
        K_m+S

This is a practical form, because K_m and Vmax can be easily measured (which is not so easy for E^o and k3).

We can also see that k3 = Vmax/E^o, =(the maximum dP/dt)/E^o, =(the maximum -dSdt)/E^o,

= the maximum number of moles of substrate converted to product per mole of enzyme per second; = max. molecules of substrate converted to product per molecule of enzyme per second (which is easier to visualize);
= the TURNOVER NUMBER (t.o.n.) of the enzyme, which is a measure of the enzyme's catalytic power.

Given that the substrate is bound, the turnover number is a measure of how good the enzyme is at facilitating the chemical reaction. {Q&A}

Turnover numbers vary widely for different enzymes.

Our succinic dehydrogenase example enzyme has a t.o.n. of 19, 19 per second.
So it takes about a 1/20 of a second to achieve the reduction of that double bond in fumarate.
That's fairly slow. Many enzymes have ton's in the hundreds or thousands.

The highest known is for carbonic anhydrase (which catalyzes the reaction: CO₂ + H₂O <---> H₂CO₃).
The t.o.n. is 600,000 sec^-1. That's 600,000 molecules of carbonic acid produced by one molecule of enzyme in one second, a speed that's hard to imagine.

How about K_m? There are several ways to look at it.

A practical way: K_m IS THE CONCENTRATION OF S THAT PRODUCES A HALF-MAXIMAL VELOCITY. Just plug this V, V=Vmax/2, into the Michaelis-Menten equation and then solve for the [S] that would give this Vmax/2. One gets: [S]=K_m.

Note that, as suggested by this equivalence, K_m does have the units of concentration (molarity).

Graphically: If we plot Vo vs. S, and look across at V0= 1/2 Vmax on the y-axis, or ordinate, and then read down to the abscissa, or x-axis, we can read the K_m right from the graph.

Our original definition of K_m, algebraically, was k2+k3/k 1, and this provides a way to look at K_m that gives us an insight into the effectiveness of an enzyme. However, it requires a simplifying assumption :

Very often (but not at all always), k2 and k1, representing the association and dissociation of E and S, are much faster than k3, so that k3 is the slow limiting step in the sequence of reactions. Since K_m = (k2 + k3)/k1, then if k3 << k2,

then K_m ~ k2/k1

Now k2/k1 is just the equilibrium constant for the reaction ES ---> E + S.

                                                            k1
To review chemical equilibria: [A] + [B] <-----> [C] + [D]
                                                           k2

The equilibrium constant K_eq = [C]_eq[D]_eq/[A]_eq[B]_eq,and this= k1/k2.
This follows from the way k1 and k2 are defined:

for production of one of the products, say C, here: d[C]/dt = k₁[A][B] - k₂[C][D]

But at equilibrium, d[C]/dt = 0 (There's no net change of any components at equilibrium, by definition)

so at equilibrium,   k₁ [A]_eq[B]_eq = k₂[C]_eq[D]_eq and [C]_eq[D]_eq/[A]_eq[B]_eq = k1/k2 = K_eq

We can choose to write the dissociation reaction of the ES complex into free E and free S from left to right, instead of the right to left way written for conversion of substrate into product:

          k2
ES <----> E + S.
          k1

So in this circumstance, K_m approximates the DISSOCIATION CONSTANT (Kd) of the ES complex.

(cf. Association constant, Ka = k1/k2 = 1/K_m)

So the higher the K_m, the more readily the ES complex will come apart, will dissociate; the higher the K_m, the poorer is the ability of the enzyme to hold onto its substrate, to BIND it.

And vice versa: the lower the K_m, the lower is the tendency to dissociate; that is, the tighter is the ability of the enzyme to hold onto its substrate, and thus BIND its substrate.

This fits with the graphical picture also: the higher the K_m, the more S you have to add to get the enzyme to go, at even 1/2 the Vmax.

Typical K_m's are 10^-3 to 10^-6molar. Some are even better than 10^-6 M. Although binding can be very efficient, there are limitations (e.g., 10^-12 M will generally not work).

And remember, the enzyme here is acting as a catalyst that can be used over and over and over. So usually the enzyme concentrations are much lower than the substrate concentrations, even at S concentrations well below the K_m.

Summary:

Enzymes increase the rate of spontanE^ous reactions, not changing their direction.

They do this by their ability to bind specific substrates to form transition state complexes.

Vmax is related to T.O.N., which is molecules of S --> P per enzyme molecule per second

K_m is related to the ability of the enzyme to bind its substrate.

A higher K_m means poorer binding.

The catalytic ability of an enzyme can be characterized by these two parameters.

Virtually every chemical reaction in the cell is catalyzed by an enzyme.

The enzyme binds its substrates with great specificity and it usually aids in the chemical reaction that takes place.

However, the enzyme itself emerges unchanged.

What is the function of these enzymes in the cell? The enzymes are central to the whole problem of building 2 new E. coli cells from one old one. Remember the flow of glucose carbon atoms into the 50 different small molecules, which go on to form the 5000 different macromolecules? Each arrow in those biosynthetic pathways represents an enzyme, a particular protein with a particular amino acid sequence, with a particular 3-D structure, which can bind and catalyze the chemical transformation of particular substrates into particular products (and having particular K_m's and t.o.n.'s). (Draw arrows and letters emanating from glucose).

::Enzyme inhibition::
Let's continue the discussion of enzymes by considering the modulation of enzyme activity, through 3 types of inhibition of an enzyme's catalytic action.

The 3 types are inhibitors I want to discuss are :

competitive (e.g., illustrating the action of drugs)

non-competitive (e.g., poisons)

allosteric (e.g., characteristic of natural feedback regulators)

::competitive inhibition::
A competitive inhibitor is a molecule that competes with the natural substrate for the substrate binding site of the enzyme. In the presence of a COMPETITIVE INHIBITOR:

At low [S], you may get good effective inhibition as long as the substrate concentration is low,
but at high [S], the competitive inhibitor (I) will be swamped out.

Let's look at this situation on our Vo vs. S plot.

At a given concentration of I, adding more and more S will eventually bring you back to Vmax, as I is swamped out.

The APPARENT K_m in the presence of the inhibitor, will be increased, reflecting the difficulty the substrate is having in getting bound to the enzyme.

It follows that since the competitive inhibitor must bind to the same site as the substrate it should have a structure VERY SIMILAR TO THE SUBSTRATE. See [Purves6ed 6.21a].

Why is competitive inhibition important? Because since we know the structure of the substrate, we, with the help of organic chemists, can design and synthesize candidate organic molecules as specific enzyme inhibitors, which can be useful in medicine.

For example, this morning, as every morning, I took 100 mg of the drug allopurinol, which has the 2-ring structure as seen on the handout.

I took it because my uric acid (see the uric acid structure in the handout) levels are too high. ..... Uric acid is not very soluble, so if the concentration in the blood is too high, it can precipitate and settle, collecting in capillaries of your feet, and you have gout, a painful condition. Or it can precipitate in the urine as it is excreted (thus the name), leading to kidney stones.

Uric acid is produced by the action of the enzyme xanthine oxidase, that catalyzes the reaction :

hypoxanthine (from nucleic acids we eat) -------> uric acid (which is excreted) (see handout)

For some unknown reason, this enzyme becomes overactive in some people, so that they overproduce uric acid.

The allopurinol can bind to the xanthine oxidase, but it cannot be oxidized (Note differences in the 5-membered ring and where the OH's are introduced). The binding of allopurinol prevents the binding of the true substrate.

So competitive inhibitors are important for pharmaceutical applications (e.g., many of the anti-HIV drugs [e.g., AZT, ddC] are competitive inhibitors of the enzymes that polymerize the viral nucleic acid).

And they are important to the biochemist, as she or he can use various analogs of the true substrate to probe the nature of the active site, to determine just what groups on the substrate are being recognized in the active site.

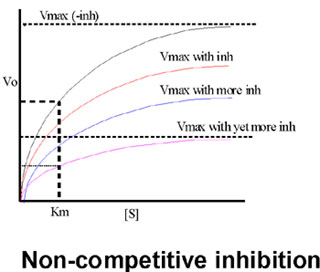
::non-competitive inhibition::
Non-competitive inhibitor, NCI:

But a chemical compound need not always look like the substrate in order to act as an inhibitor. A non-competitive inhibitor can binds to a site other than the substrate binding site and inhibit activity. These inhibitors usually interfere with the catalytic reaction itself (the formation of a transition state complex on the surface), so the substrate still binds to the enzyme, but then the enzyme can't do anything with it. Take, mercury (Hg), for example; unlike allopurinol, it is a poison rather than a therapeutic agent. Hg can bind to free sulfhydryl groups, which in proteins means the side chain of cysteine. Sulfhydryls often take part in the catalytic process, but if Hg is bound the sulfhydryl may not be able to do its job. In this case, adding an excess of substrate will NOT reverse the action of the inhibitor. The Vmax of the reaction will be affected, but not the K_m.

How will a non-competitive inhibitor affect the measurement of enzyme kinetics?

Graphically, we can see that at a given concentration of inhibitor, we get a lower Vmax, and the higher the concentration of the non-competitive inhibitor, the lower is the achievable Vmax.

How can we envision this?

Think of a beaker of enzyme. If we add an excess of non-competitive inhibitor, we cannot measure any activity, so we cannot investigate any effect. So let's add a sub-saturating amount of non-competitive inhibitor. At any given moment, a constant proportion of the enzyme molecules will be taken out of action because they are binding the non-competitive inhibitor . Let's say 2/3 are inactive at any moment (but in a dynamic equilibrium):

The remaining 1/3 are OK and act perfectly normally with respect to their dependence on S. It is they that contribute to the V being measured on the graph.

So the K_m measurement is not affected; this uninhibited fraction of the enzyme population gets to 1/2 of the new (lower) Vmax that can be attained at the usual S concentration. But the Vmax they attain will be only 1/3 of that reached in the absence of the non-competitive inhibitor. So here the apparent Vmax is lowered and the K_m is unaffected, just the opposite of what we saw with a competitive inhibitor.

::allosteric inhibition::
The third type of inhibitor is called an ALLOSTERIC INHIBITOR. This is the most important natural enzyme inhibition. Living cells use enzyme inhibitors to regulate the activity of many enzymes. This kind of inhibition is similar to non-competitive inhibitor, in that the inhibitor binds to a site different from the substrate binding site. In this case it binds to its very own special site, remote from the substrate binding site, and acts by deforming the enzyme so that it either can no longer bind its substrate or cannot catalyze its reaction. Enzymes that are regulated by allosteric inhibition are usually hetero-multimers composed of regulatory subunits and catalytic subunits. The allosteric inhibitor binds to the regulatory subunits in a reversible manner changing their conformation. The catalytic site on another subunit is turned on or off depending on the conformation of the regulatory subunits. The quantitative treatment of this inhibition is beyond our scope here. But see Purves6ed 6.23 for a picture.

SO: Allosteric inhibitors (black ball in the diagram) can affect the apparent K_m, Vmax, or both. {Q&A}

How does the cell use this allosteric inhibition?

::Feedback inhibition::
The most obvious roles in the E. coli cell are for those enzymes that catalyze the reactions of a biosynthetic pathway.

E. coli growing on glucose as the only source of carbon must synthesize all of its small molecules by a series of chemical reactions that emanate from glucose. In general, glucose is first broken down from its 6-carbon state to smaller molecules of 3, 2 or 1 carbons, and then these smaller molecules are then used to build all the necessary monomers and co-factors in the cell.

All the monomers, the 20 amino acids, the prosthetic groups like heme, virtually every molecule in the cell has a pathway that can be traced back to glucose. These pathways do not simply run at equal and constant rates, but rather are tightly controlled and coordinated. Much of this coordination is brought about by the cell's judicious use of allosteric inhibition. The very molecules that are being synthesized (the end-products of the pathway) are often used as the mediators of this inhibition; they are the allosteric inhibitors, as we will see in a moment.

A pathway traced back from an end-product to glucose can usually be divided into two parts, the breakdown part, called catabolism, and then the build-up part, called anabolism.

Or catabolic pathways vs. anabolic pathways (the anabolic pathways are more often called biosynthetic pathway or biosynthesis).

So: Glucose ---->

Each arrow in the diagram represents a specific chemical transformation, such as the reduction of fumarate by succinic dehydrogenase, or the oxidation of hypoxanthine by xanthine oxidase.

To coordinate all this activity, E.coli has evolved a sophisticated and sensible way of controlling the flow of glucose carbons through its biosynthetic pathways. This is called end-product inhibition, and usually works by having the end-product of a biosynthetic pathway act as an allosteric inhibitor of the first step in the pathway that is committed to the biosynthesis of that molecule (e.g., G for rxn. 5, N for rxn 10 in the diagram above). That is, the first enzyme in a pathway has evolved to have, built into its structure, a site for the ultimate end-product of the pathway it is starting. Since the end-product is usually many steps down the road of chemical transformations, it does not bear much resemblance to the substrate or the product of the reaction it is inhibiting. See [Purves6ed 6.24].

For example, the pathway to the amino acid isoleucine can be considered to start as a branch after the synthesis of the aa threonine:

                                               Thr deaminase
glucose ...... --> --> threonine -----------------> alpha-ketobutyric acid --> A --> B --> C --> isoleucine (and no other aa)

Isoleucine turns out to be an allosteric inhibitor of the enzyme threonine deaminase

In this way the pathway to isoleucine is shut off when enough isoleucine is present - the cells has feedback information about the amount of end-product it is synthesizing. This mechanism of feedback inhibition or end-product inhibition is used extensively in E. coli to avoid the waste of running a pathway when it is not needed.

Does this mean that E. coli could divide a bit faster if we gave it isoleucine in addition to glucose in minimal medium? Could it shave its doubling time from 60 minutes down to say 55 minutes by shutting off that path? While we're at it, why not add all 20 amino acids, and a few vitamins, some fatty acids, some DNA and RNA precursors. Now would E. coli grow any faster? Indeed they do, in such a rich medium they will double every 20 minutes, instead of once an hour. A whole new E. coli cell in 20 minutes. Now feedback inhibition is not the only reason for this increased efficiency, but it is playing a large part. And you can imagine that this ability to shut-off off and turn on biosynthetic pathways fits the life style of E. coli as it sits in your intestines waiting for the next Big Mac. The more efficient doublers will soon take over the population, so there probably has been great selective pressure for the evolution of these control mechanisms that respond to the environment in this way.

One can see why you need the allo-steric ("different in space") inhibition mentioned above for the feedback regulation of this biosynthetic pathway. Note that the inhibitor, isoleucine, bears little resemblance to the substrate (threonine) for the reaction it inhibits. Isoleucine binds not to the catalytic site (active site) but to an allosteric site, a special regulatory site that is remote from the catalytic site. Indeed, in the regulatory site is located on a separate polypeptide in threonine deaminase, a protein with quaternary structure.

(C) Copyright 2001 Lawrence Chasin and Deborah Mowshowitz Department of Biological Sciences Columbia University New York, NY
Clickable pictures are from Purves, et. al., Life, 5th Edition, Sinauer-Freeman's Images of Life 5.0.
A production of the Columbia Center for New Media Teaching and Learning