Biology C2005 Lecture 8

::Free energy, delta G and delta Go::
We now have some idea of how the rate of chemical reactions in the cell are speeded up so that they can occur in time frames consistent with cell growth. But what about this problem of DIRECTION, a problem the catalysts cannot address. Are all the chemical transformations in these biosynthetic paths, for example, exergonic, so that the direction of carbon flow from glucose is a spontaneous reaction? The answer is no, quite the opposite. Most of the chemical transformations needed in a biosynthetic pathway are by themselves endergonic, and will not go from left to right unless something is done about it. Thus the building of a new E. coli cell must deal with this energy problem, and much of the cell machinery has indeed been devoted to the solution. To understand the problem, we must discuss it in some more quantitative detail, and for this purpose, the use of the concept of FREE ENERGY CHANGE associated with a chemical reaction is very useful.

We can define a unit of energy such that it is tied to the directionality of a chemical reaction as follows:

For the model reaction A + B <--> C + D, written in the left-to-right direction indicated:

IF Delta G IS <0 THEN A AND B WILL TEND TO PRODUCE C AND D.

IF Delta G IS >0 THEN C AND D WILL TEND TO PRODUCE A AND B.

IF Delta G IS 0 THEN THE REACTION WILL BE AT EQUILIBRIUM: NOT TENDING TO GO IN EITHER DIRECTION IN A NET WAY.

In an energy diagram:

Note that the Delta G is independent of the route between the starting reactants and the final products (say, 3 kcal/mole, for all 4 routes shown here).

Free energy is that part of the energy change associated with a chemical reaction that can be harnessed to perform work.

We can measure Delta G according to the following equation [must take this on faith here]:

Delta G = Delta Go + RTln([C][D]/[A][B])

where A, B, C and D are the concentrations of the reactants and the products AT THE MOMENT BEING CONSIDERED.

This ratio is sometimes called Q (so Delta G = Delta Go + RTlnQ).. Q is NOT the equilibrium constant, though it looks like it...:

Here are the terms:

R = UNIVERSAL GAS CONSTANT = 1.98 CAL / DEG K MOLE
T = ABSOLUTE TEMP. (0^o C = 273^o K; Room temp = 22^o C = 298^o K)
ln = NATURAL LOG
Delta G^o = A constant, a QUANTITY RELATED TO THE INTRINSIC PROPERTIES OF A, B, C, AND D. {Q&A}

The first term, delta G^o, relates to the QUALITY of the reactants and products, and the second term, RTlnQ, relates to the QUANTITY of the reactants and products, how much of each is present.

What is this Delta G^o? It is called the: STANDARD FREE ENERGY CHANGE of a reaction.

One useful way to define of it is to consider the special case when all the reactants and all the products are present at 1 unit concentration. The change in free energy of this reaction is:

Delta G = Delta G^o + RTln(1), or Delta G = Delta G^o +RT x 0,

or delta G = delta Go (a special case when all participants are at 1M)

So Delta G^o is the free energy change that occurs when all participants in the chemical reaction are at unit concentration. What is unit concentration? 1 M, for most reactants and products (water and hydrogen ions are treated differently, as we'll see. )

One way to think of this delta G^o is to picture 1000 moles of A, B, C and D in 1000 liters of solution. So all components are at 1M. One mole of A + B is now converted to C +D. The energy absorbed is the standard free energy change. Note that the concentration of reactants has not appreciably changed in this hypothetical condition.

Why make such a fanciful and arbitrary situation? By defining the conditions for a STANDARD free energy change, all reactions can be compared to one another, regardless of the particular conditions; it puts them all on an equal footing. The Delta G^o reflects the nature of the reactants and products without regard to their concentration. Note that the actual free energy change of a reaction does depend on these concentrations, and the SECOND TERM of the equation for delta G takes these into account. {Q&A}

Please note from the above explanation that delta G and delta G^o are not the same thing. That distinction is important.

::Equilibrium::
Delta G^o can be calculated, although not accurately, from tables of free energies of formation from simple atoms or molecules, comparing these values for the reactants and the products. But it is most easily and accurately determined experimentally, by measuring the concentration of the reactants and products at equilibrium. For at equilibrium, Delta G = 0 and

Q = K_eq, (a special case). So: Delta G^o = -RTlnK_eq.

If we measure A, B, C and D at equilibrium, let's say we get: [C]_eq[D]_eq/[A]_eq[B]_eq =
2.5 x 10-3

Note very little C and D are formed from A and B in this case.

Then Delta G^o = -2 x 300 x ln (0.0025) = -600 x -6 = 3600

So the calculated Delta G^o is +3600 cal/mole, or +3.6 kcal/mole. So 3.6 kcal will be absorbed when 1 mole of A + B goes to C + D. Energy is absorbed rather than released, confirming the lack of a tendency of C and D to be formed from A and B.

That is, since the standard free energy change is positive, this reaction does not tend to go to the right, but rather to the left. That is, if we start with 1M A, B, C and D, then C + D --> A + B. So A and B will build up at the expense of C + D.

Note:
If we write A + B --> C + D, Delta G^o = +3.6 kcal/mole, then we can also write:
C + D --> A + B , Delta G^o = -3.6 kcal/mole (the equilibrium constant for this C+D -->
A+B reaction is just 1/2.5 x10^-3, or 400)

Note also, that if the reactants combine in ratios other than 1:1, we can write:
aA + bB <--> cC + dD, Delta G = Delta G^o + RT ln [C]^c[D]^d
                                                                           [A]a[B]b

::Summary of free energy changes::
And to reiterate: the free energy change of an overall reaction is independent of the route taken by the reactants, it could be direct or indirect [see energy diagram with routes that go up or down to intermediates].

The reaction will go to the right if delta G is <0 and to the left if delta G is >0. At delta G = 0 the reaction is at equilibrium, and under this special condition (delta G = 0) Q is equal to the K_eq.

We stated that delta G^o is called the STANDARD free energy change and represents the free energy change when these reactants and products are observed to react with each being at a concentration of 1M, which is the standard condition, by definition. However, biochemists make 2 exceptions to the definition of these STANDARD CONDITIONS in the cases of water and hydrogen ion concentration. Since these two components in a reaction are usually constant in a biological reaction, they are defined to be equal to 1 for the purpose of Delta G^o calculation when [H₂O]=55M (pure water) and [H+] = 10^-7 M (i.e., pH7, or neutrality). Strictly speaking, one should acknowledge this use of these 2 exceptions by designating the free energy change as delta G^o' rather than delta G^o, but we will not bother to do that here.

All chemical reactions have a Delta G^o associated with them, a value which can be written down in a book. Thus any two reactions can be compared under the standard condition of unit concentration.

The equilibrium constant of a reaction can be easily measured by measuring the concentration of all reactants and products after the reaction has reached equilibrium. From the equilibrium constant, one can calculate the Delta G^o of the reaction, since at equilibrium, delta G = 0, and so Delta G^o = -RTlnK_eq.

Whereas the first term in the equation for delta G takes into account the nature of the reactants, the second term deals with the amounts of the reactants and products in the situation under consideration. Thus if you know what you have and how much of each, you can predict the direction in which the net reaction will go.

::ATP hydrolysis::
To start our consideration of the free energy changes that are associated with biochemical reactions, let's consider one of the most important and fundamental energy-related biochemical reaction, the hydrolysis of adenosine triphosphate, or ATP. Hydrolysis means the breakage of bonds by the addition of water. Here:

where A = adenine (a base); R = ribose, a 5C sugar; joined to 3 phosphate groups, which are themselves joined together. See [Purves6ed 6.8].

The Delta G^o of this reaction is about -7 kcal/mole.

::"High energy" bonds ("~")::
Most HYDROLYSIS reactions in the cell do release free energy, but usually less than 5 kcal/mole. The few, like ATP hydrolysis, that release more than 5 kcal/mole, are important, because this amount of energy can be harnessed for useful work, as we'll see. The bonds whose HYDROLYSIS IS 7 KCAL/MOLE OR MORE ARE CALLED "HIGH ENERGY BONDS" for this reason. These bonds are not stronger than other bonds, so this is somewhat of a misnomer, but it turns out to be a convenient term. It is denoted by a SQUIGGLE when we are talking about it: AR-P-P~P. Looking at the structure of ATP we can rationalize the high energy release by seeing that the addition of water relieves the electrical repulsion between the negatively charged (acidic) phosphate groups. By such reasoning we would predict that the bond between the first and second phosphates should also be a high energy bond, and indeed it is, so:

AR-P~P~P. That is, hydrolyzing between P atoms 1 and 2 also releases about 7 kcal/mole (i.e., delta G^o = -7kcal/mole)

On the other hand the bond between the ribose and the first phosphate is not a high energy bond.

Given the Delta G^o, one can calculate the equilibrium constant, which turns out to be about 10⁺⁵.

(-7 = RT x 2.3 log K = 0.6 x 2.3 log K; K =10^(-7/-1.4)= 10⁵).

You should practice these types of calculations by doing the problems in Problem Set 4.

(In doing these problems, note that the universal gas constant is usually given as 1.98 cal/deg-mole, whereas Delta G^o and delta G are usually expressed in kilocalories, so you usually have to divide the RT term by 1000 to get an answer in kcal.)

I will just note that the concentration of WATER is not taken into account, as it is present at 55 M in aqueous solution and does not CHANGE in aqueous reactions, and by convention is defined as 1. (We can make such arbitrary definitions because we are only considering changes here [concentration changes, free energy changes], not absolute values.)

So if we start with 1M ATP we will end up with only about 10^-5 M ATP remaining at equilibrium.

Yet a 1 ml. solution of ATP will last for days on this bench top. We still must add a catalyst to get this reaction to go in a reasonable time.

So we add an enzyme, say a pure preparation of ATP-ase (note nomenclature).

Now all the ATP is hydrolyzed in a few minutes. The reaction has been allowed to reach its equilibrium and has gone far to the right, because of the very favorable (large and negative) delta G.

And 7 kcal of energy, free energy, is released. Free energy, so it could be used for useful work, but what work did it do here? Nothing? Energy had to go somewhere. It is released as HEAT. The test tube solution warmed by about 7^oC, by my calculation [since 1 ml of solution here, at 1 M].

This hydrolysis of ATP is in fact the most common reaction the cell uses to produce usable energy. The trick is to harness this energy chemically, to put it to useful chemical work. Keep in mind the overall problem, to make a new E. coli cell that requires many endergonic transformations.

::Coupled reactions::
So let's take an example of one of these endergonic energy-requiring reactions: One such reaction is the very first transformation that a glucose molecule undergoes upon entering an E. coli cell:

+ P_i --> glucose-6-P + H₂O; Delta G^o = +3.6 kcal/mole.
(Note that Pi is used as an abbreviation for PO₄---)

So the Delta G^o is unfavorable in the very first reaction in the utilization of glucose in the cell.

How bad is the situation?

G + Pi --> G-6-P, Keq = [G6P]/[G][Pi]

If [G] and [Pi] are ~ 0.01M (typical) and Keq (from Delta Go of +3.6) = 2.5 X 10-3 then [G6P] = 2.5 x 10-7, which is even below the Km's of most enzymes (for example, for the next reaction taking G6P further). Now let's consider putting the two reactions we've talked about together: ATP + H2O --> ADP + P_i Delta G^o = -7 kcal/mole
Glucose + Pi --> G6P + H2O Delta G^o = +3.6 kcal/mole
-----------------------------------------------------------------------------
Glucose + ATP --> G6P + ADP Delta G^o = -3.4 kcal/mole overall = net sum of the two considered reactions

So let's mix the reactants together and hope for the best.... I guess we should add a couple of enzymes to catalyze these 2 reactions: say: "glucose phosphorylase" and "phosphatase".... But under these conditions the 7 kcal/mole produced by the hydrolysis of ATP is lost mainly to heating the surroundings (H₂O). And besides, in mammals, where E. coli lives, the temperature is kept constant, so we cannot influence reactions by heat. The problem is solved by an enzyme, hexokinase. This enzyme binds both ATP AND glucose. The very phosphate from the ATP is transferred to the glucose molecule. So the overall reaction written here on the bottom line is not merely the net sum of the two reactions written above it, rather, it IS the reaction catalyzed by hexokinase. The phosphorylation of glucose has been COUPLED to the hydrolysis of ATP. {Q&A}

What about the G6P produced? Does it now contain the high energy phosphate bond? Well, what is the Delta G^o for G6P hydrolysis? Easy: -3.6 kcal/mole, since reverse reaction (second line) is +3.6. But -3.6 falls short of the -5 needed to qualify for a high energy bond, so no squiggle here. Remember, if you write a reaction backwards, you just reverse the sign of the Delta G^o.

This coupling to ATP hydrolysis is a very common way the cell uses to drive otherwise endergonic reactions. [Purves6ed 6.9] Since the ATP is so often used to "pay for" the energy cost of these chemical transformations, ATP is called the energy "CURRENCY" of the cell. Coupling to ATP is one of two ways the cell manages to run endergonic reactions; we will discuss the second way a little later.

So is this the solution for E. coli growing on minimal medium? Far from it; we have just passed the buck. Where's this ATP coming from? Not from the medium, where glucose is the only carbon source. ATP must be synthesized from glucose just like all other small molecules. And that itself takes energy. But, once we have some ATP, most of the molecule can be used over and over again to provide energy for coupled reactions, as long as we can re-phosphorylate ADP back to ATP. The problem has thus shifted to this reaction: ADP + Pi --> ATP (Delta G^o = +7 kcal/mole). If we could find a way to do that, we would have solved our energy problem.

Here is where we have some divergence in the unity of biochemistry: The world is divided mainly into two types of organisms, those who can run this reaction using the energy derived from sunlight, the photosynthetic organisms, like plants; and the rest of us, E. coli, humans, butterflies, who make ATP from ADP by using the energy derived from the breakdown (catabolism) of carbon compounds like glucose. Plants are actually also included in this latter category, since when it's dark they derive energy from glucose catabolism, as the rest of us do. We will consider this process of glucose-based energy metabolism in some detail, and not really consider PHOTOSYNTHESIS, for lack of time. Obviously, photosynthesis is the more basic and essential process for the planet, since there would be no glucose if it were not for the plants and their ability to harness solar energy. But photosynthesis is a bit more complex, so it is not a good place to start.

So, ATP by way of glucose:

The overall plan is (for E. coli growing in air [dissolved oxygen]):
glucose + O₂ --> CO₂ + H₂O, and: ADP + Pi --> ATP

First, an overview: 3 parts: In each of these 3 parts we will be concerned with our goal: to produce ATP's for use in reactions that require energy.

1) GLYCOLYSIS: in which the 6C glucose is broken down to a 3C compound, pyruvic acid [glucose (6C) --> pyruvate (3C)].

2) THE KREBS CYCLE, in which the pyruvate is broken down to CO₂ [pyruvate --> CO₂]

3) The ELECTRON TRANSPORT CHAIN, in which oxygen is taken up and water is produced in a separate series of reactions [utilization of O₂]

I am now going to discuss GLYCOLYSIS in some detail, for two reasons:

1) It will illustrate the problems and the solutions of energy requirements, so one aim is to understand energy metabolism.

2) It is a real life detailed example of a typical metabolic pathway,such as we have been alluding to with all these arrows leading to A's and B's and C's. (The pathway will be characterized by a series of small changes between substrate and product at each step)

::Glycolysis::
I'll show the first few reactions with the sugar in open chain form, because I think it is easier to see what's going on.

1. a phosphorylation (kinase enzyme)

2. an isomerization

3. phosphorylation again... note that we have now used 2 ATPs: rather than generating energy, we are consuming it, so far.

4. hydrolysis

5. isomerization of dihydroxyacetone phosphate (as we saw in step 2, but in reverse, transforming the ketone into the aldehyde; and swing it upside down when done: you have another molecule of glyceraldehyde-3-phosphate): note now we have 2 of everything for each glucose molecule that entered the pathway, this will be true from this point on.

So, so far, through rxn 5, we've produced 2 molecules of glyceraldehyde-3-phosphate (GAL-3-P) for each molecule of glucose we used. AND it so far has COST us 2 ATP's This ATP debt is a loose end that we will have to deal with sooner or later.....

6. Step 6 is an oxidation, GAL-3P and another phosphate to 1,3 diphosphoglyceric acid, (or 1,3-diPGA).

OXIDATION, the loss of ELECTRONS. We saw it before in the formation of the disulfide bond - there the loss of two electrons was in the two hydrogen atoms that were taken away. Here, in reaction 6, we have 2 electrons to be lost from the reactants, GAL-3-P and phosphate:

::NAD::
Two electrons have been lost. The protons are not important in oxidation, they are sometimes there with the electrons, and sometimes not. {Q&A}. These electrons must go somewhere. They are taken up by the OXIDIZING AGENT which itself will get reduced. As you can see from the NAD handout, this is a compound called NAD, or NICOTINAMIDE ADENINE DINUCLEOTIDE [Purves6ed 7.3]:

The nicotinamide part is also the vtramin niacin. Niacin sounds less ominous.

In getting reduced, NAD can accept two electrons, but only one proton. The other proton goes into solution as a hydrogen ion. But it is the electrons that are important in oxidations.

Instead of writing the reduction of NAD as NAD+ --> NADH + H+, we will simply write: NAD --> NADH₂, referring to the two H's that came from glyceraldehyde-3-phosphate, despite the fact that both proton did not end up on NAD. {Q&A}

This rxn 6 is rather complicated, involving a phosphorylation as well as an oxidation. The phosphorylation did not require an ATP, but it did require an NAD.... so now have a new loose end analogous to the ATP/ADP situation, we have to worry about restoring NADs from NADH2's as well as ATP's from ADP's.

But at least we have something of value here, a high energy phosphate, as you can see the squiggle at the top of 1,3-di-PGA on your glycolysis handout. That means that enough energy can be released from the hydrolysis of this phosphate even to drive the phosphorylation of ADP in a coupled reaction.

Let's take the money and run... this high energy bond is cashed in the next reaction, rxn 7.

7. Note that the top carbon is now a carboxylic acid in 3-PGA, whereas it had been an aldehyde in GAL-3-P. This change is the result of the oxidation that took place in reaction 6. {Q&A}.

So we've now paid off one of the 2 ATPs the debt we ran up at the start. Wait a minute, actually, we're all paid up (since we have two di-PGA's for every mole of glucose that started down the glycolytic pathway).

Continuing along:

8. Isomerization of 3-PGA to 2-PGA.

9. Dehydration, water removed. The result is an unstable compound, phospho-enol pyruvic acid (PEP), one whose hydrolysis can result in the release of a large packet of free energy.

    [2-PGA, as well as PEP, is at a higher energy level than pyruvate, but the shift in atoms allows
    cash-in of ATP along the way, since the phosphate bond is a high energy bond in PEP.]

10. Transfer of the phosphate to ADP (X2), resulting in PYRUVIC ACID (pyruvate), which can be considered the end point of glycolysis. [Purves6ed 7.7a], [Purves6ed 7.7b], [Purves6ed 7.7c].

So after the 10 steps of glycolysis we have 4 ATPs produced and 2 invested, for a net gain of 2 ATPs produced from ADP. So glycolysis does produce energy in the form of ATP. And the overall reaction will run far to the right, as the Delta G^o from glucose to 2 pyruvates is -18 kcal/mole (even taking coupled reactions producing the 2 net ATP into account). That is,

1 glucose + 2 ADP + 2 Pi + 2 NAD <--> 2 pyruvate + 2 ATP + 2 NADH₂

Delta Go = -18 kcal/mole

The diagram below shows Delta G^o's for the individual steps in glycolysis.

(For a different way of looking at it, see the chart of Delta G's drawn by Purves [Purves6ed 7.6])

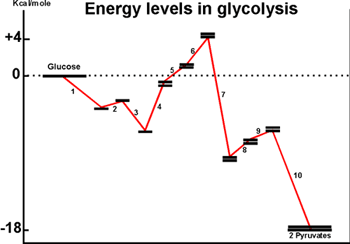
Although the pathway overall is quite favorable, some individual reactions are quite unfavorable, the most extreme being reaction #4. The energy-requiring reactions in this case are being pushed by the build-up of reactants by the more favorable reactions before them, and they are being pulled by the withdrawal of products by the more exergonic reactions further downstream. The actual Delta G's will be influenced by the drain of products, so that the second term in the equation for Delta G is being brought into play here.

Delta G = Delta G^o + RTln([products]/[reactants]), where RT~0.6 (in kcal/deg-mole)

For instance, if the products are drained such that the ratio of P/R reaches down to 0.00001, this produces ~ 7 kcal/mole of negative Delta G , enough to balance out the unfavorable Delta G_o of +6.8 for rxn 4.

This indirect affect on the Delta G is the second method the cell utilizes to carry out an individual reaction that has an unfavorable Delta G^o.

So we have 2 methods:

1.) DIRECT COUPLING of the unfavorable reaction to an energetically favorable one to produce a new coupled reaction with a net negative (favorable) Delta G^o (as in the hexokinase reaction #1).

2.) INDIRECTLY, via the WITHDRAWAL OF PRODUCTS or buildup of substrates

SO, we have our overall negative Delta G^o , and we have generated net ATP, so we should feel pretty good, except for one thing: we have an important loose end to tie up. We borrowed an NAD to oxidize Gal-3-PO₄. That was a key reaction in the path, as oxidations are usually accompanied by large changes in free energy. We were able to get a PO₄ added to our 3-carbon compound, and this phosphate was the one that was used to phosphorylate ADP in the very next step (#7). We used NAD, and it became reduced to NADH2. So now we must consider how we are going to repay that debt. Otherwise the small stores of NAD in the cell would very soon all be converted to NADH₂ and glycolysis would quickly grind to a halt.

We need an oxidizing agent to oxidize NADH₂. A great one abounds: O₂.

It readily takes up electrons, for instance from Fe++ to make it Fe+++ as steel goes to rust.

::Anaerobiosis::
Does E. coli have access to oxygen? In the lab, yes. We vigorously and constantly shake the E. coli cultures on mechanical shakers to get air dissolved in the culture medium to provide a constant source of oxygen, called an AEROBIC state. In the gut, sometimes yes, sometimes no (crowded). Do our own cells have access to oxygen? Sure, through the lungs via the blood vessels to all tissues. But when you are running across campus to class so as not to miss the first golden words here, your muscles may need ATP faster than you can deliver oxygen to them for NADH₂ oxidation, your muscles will be in an AN-AEROBIC state. And are many organisms that live in naturally anaerobic environments, in mud at the bottom of rivers, e.g. So let's first consider the anaerobic case when no oxygen is available for the oxidation of NADH₂. Under these circumstances the cell must make do with what it has available, which is mainly: 2 pyruvates. Fortunately, pyruvate itself is able to act as an oxidizing agent, as seen in rxn 11, where it accepts electrons into its C=O bond, adding two hydrogens as well, to form lactate, or LACTIC ACID. It gets the electrons from our NADH₂ molecule, which is really NADH and H+, so it is recapturing one proton (an H+ ion) from the aqueous pool. Even the Delta Go is favorable, and we get our NAD regenerated from NADH₂. The NAD shuttles back and forth then, getting reduced in rxn 6 and reoxidized in rxn 11 over and over and over again, while glucose runs down to lactate, and ADP's are converted to ATPs to power cell division for E. coli or running up stairs for humans even in the case of insufficient oxygen.

I think it's the build-up of lactic acid that makes your muscles hurt if they are doing anaerobic glycolysis too long.

::Fermentation::
So pyruvate is a crossroads: If no oxygen, then if you are E. coli or humans, you carry out a lactic acid fermentation... [Purves6ed 7.5b], [Purves6ed 7.15].

If you are yeast, there is a variation on this theme, you break down pyruvate first to acetaldehyde and CO₂, which is not an oxidation, but then use the acetaldehyde as an oxidizing agent for NADH₂, with the product here being the 2 carbon alcohol, ethanol (rxns 12 and 13). Beer drinkers appreciate this variation, as lactic acid beer would be pretty bad, and probably not even produce those psycho-pharmacological effects for which ethanol is famous. {Q&A}.

Just as in the case of ATP, the NAD - NADH2 case is one of re-generation, not generation. Once a little NAD is made, it can shuttle back and forth millions of times getting alternately reduced and oxidized:

Consider the efficiency of fermentation:

For: glucose--> 2 lactates, without considering the couplings for the formation of ATP's: Delta G^o = -45 kcal/mole. {Q&A}.

Out of this comes 2 ATPs, worth 14 kcal/mol. So the efficiency is about 14/45 = 30%, which is not bad, about what a gasoline engine can do.

Where did the other 31 kcal get to? They are released as heat, which is why, after you've run fast to class, in addition to the lactic acid PAIN in your legs, you are also SWEATING.

Now taking the ATPs into account, the overall Delta G^o is about 45 - 14 = 31 kcal/mole, so the lactic acid fermentation runs essentially completely to the right (or clockwise) as written.

::Energy yield::
The efficiency is pretty good, but on the other hand the YIELD is poor. What do I mean by YIELD? Well, glucose has a lot more chemical energy in it than we are tapping here. For example, if we BURN glucose (i.e., react it with oxygen) and measure the calories of heat given off, we get no less than 686 kcal/mole. Compare that to the measly 45 kcal/mole we got from converting glucose to two lactates. The lactic acid that we are throwing away at the end could be used for more energy, but in the absence of oxygen there is no way to use it.

(C) Copyright 2001 Lawrence Chasin and Deborah Mowshowitz Department of Biological Sciences Columbia University New York, NY
Clickable pictures are from Purves, et. al., Life, 5th Edition, Sinauer-Freeman's Images of Life 5.0.
A production of the Columbia Center for New Media Teaching and Learning