Scientific Notation: Powers of Ten

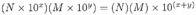
Annotation category:
Chapter 1

Note:

To appreciate the utility of scientific notation, let's start with a simple example. Using nothing but a pencil and piece of scrap paper, perform the following operations: 

1. Add 5 and 3.
2. Divide 100 by 52, to the 
   nearest tenth.
3. Subtract 503 from 10300.
4. Multiply 34,074,000,000,
   000,000,000,000,000 by
   0.0000000000000000000000
   000000000000000000000000
   0000000000732.
Having any trouble?

Chances are you were breezing along pretty smoothly until you came to problem 4. When numbers fall within a scale that you can intuitively grasp, it's sufficient to represent them with the symbols you've known since kindergarten. But the range of numbers one works with when exploring the Universe's full scale is so overwhelming that a new method of representing them becomes essential.

Scientific notation is such a method, and in science it's as imperative as elementary school multiplication tables. The general form of a number in scientific notation is:

N x 10x,

which in words reads: N times 10 raised to the power of x, where x is called the exponent, or power of 10. To convert an ordinary number to its scientific notation counterpart, here's a two-step process:

1. Locate the decimal point of your number, and move it either to the right or to the left, so that there is only one non-zero digit to the left of it. This new number is your N.

2. Count the number of spaces you just had to move your decimal point. If you moved to the left, then each space adds 1 to x (where x begins at zero.) If you moved to the right, then each space adds -1 to x. 

EXAMPLE 1: 5,230,400.00
For step 1, you need to move the decimal point 6 places to the left. The number now reads: 5.23040000, or 5.2304 (since any trailing zeroes may be dropped.) So 5.2304 is your value of N.

For step 2, recall that you have moved 6 placess to the left, so that your value of x = 6. So your number in scientific notation is: 5.2304x106, or "5.2304 times 10 to the sixth (power.)" 

EXAMPLE 2: 0.00038
This time, you move the decimal point to the right, 4 spaces. N = 3.8 and x = -4. So your number in scientific notation becomes: 3.8x10-4, or 3.8 times 10 to the negative-fourth (power.)

Once you have converted your number into scientific notation, you will find that computations become much easier. Here are five rules that numbers in scientific notation obey: 

MULTIPLICATION:

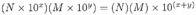
EXAMPLE: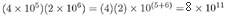

DIVISION:

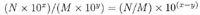
ex:

ADDITION and SUBTRACTION:

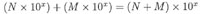
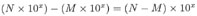
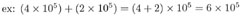
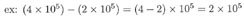
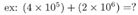
This one's trickier. In the first number being multiplied, 10 is raised to the power of 5, while in the second number, 10 is raised to the power of 6. To add these two numbers, we need to write them both using the same exponent. So we'll need to change the form of one of them. We'll (arbitrarily) choose the first number, and change (4 x 105) to a form with exponent 6 instead of 5. Remember that for each decimal shift to the left we add +1 to the exponent, and for each shift to the right we add -1. Since we want to add +1 to our exponent of 5, we move the decimal point once to the left, and our number becomes: (0.4 x 106.)

Now both numbers have the same exponent value of 6. Adding them, we find:

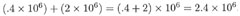
EXPONENTIAL OPERATIONS

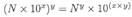
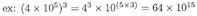
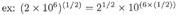
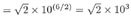
(Recall that raising a number to the power 1/2 is equivalent to taking the square root.)

RAISING TO THE POWER OF ZERO

One special case is worthy of being noted here: raising a number to the power of zero. You might think that anything raised to the power of zero would be zero. But consider the problem that that would cause:

Anything divided by itself is 1. In particular,
(103)/(103) = 1.
But (103)/(103) can be expressed as (103)(10-3),

and by the rule of adding and subtracting exponents,
(103)(10-3) = 10(3-3)
which = 100; therefore 100 must equal 1.

For more information on powers of ten, visit:

Find this term in:  


Web Resources:
  1. Powers of Ten web link