Cancelling Units

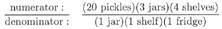
Annotation category:
Chapter 1

As an example of a dimensionless calculation (one in which you don't need to use units), add 6 + 2. It's 8. 8 what, you ask? 8 nothing. Just plain 8.

Now let's perform a calculation involving a physical scenario. Say we buy some tangerines: I buy 6 and you buy 2. What have we bought together? 8 tangerines. Not merely 8, but 8 tangerines. Tangerines are our units. Units indicate what the numeral 8 represents.

Here's a more complicated example. Compare the dimensionless calculation:

(1/8) x 16 = 2 

Let's write this word problem in a form that's easier to manipulate:

   [(1 mi)/(8 min)] x (16 min)/1]

When you multiply fractions, the numerators multiply together, and the denominators multiply together. So our problem can be written as:

   [(1 mi)x(16 min)]/[(8 min)x1]

where 1 is the implicit denominator of (16 minutes)

   = (16 mi x min)/(8 min).

Now, to simplify this fraction, we are allowed to cancel out any unit that appears both in the numerator and in the denominator. Here, we see that "minutes" appears in both places. Thus we erase the "minutes" and are left with:

   (16 mi)/8.

Dividing 16 by 8, we get 2. So our simplified answer is:

   (2 mi) / 1, or (2 miles).

Finally, let's check our units, to be more confident that we have found the correct answer. Recall that the question asked us how far we ran. So our answer should be in units of distance -- and it is. This method of dimensional analysis, or unit analysis, is a useful guideline if you are unsure of your answer.

Let's try a few more examples.

MULTIPLYING and DIVIDING WITH UNITS:

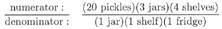
Cancelling any unit that appears on both the top and the bottom:

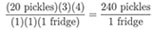
2. (1 gram of gold) / [(196.97 grams / mole of gold) x (1.66 x 10-24 moles / atom)]

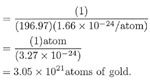
ADDING or SUBTRACTING WITH UNITS:

Here, the quantities involved and the sum they produce must all have the same units. You can appreciate this rule intuitively, by realizing that it is the only condition that makes physical sense. Consider, for example, adding 2 tangerines and 3 atoms of gold. What does that give you? 5? 5 what? No, you can only say that you still just have 2 tangerines and 3 atoms of gold. Simplification isn't possible.

ex:  3 seconds + 5 seconds 
     = 8 seconds.
ex:  5 meters - 12 meters 
     = -7 meters.
ex:  4 degrees Celcius + 18 lbs 
     = ??