Biology C2005 Lecture 1

::A biochemist's view of biology::
Biology is the study of living things, an attempt to understand how living things work.

Understand... is a word that means different things to different people.

Understanding something in science means verifiable prediction.
Quantitative predictions are the most satisfying.
Let me tell you in a general way what I mean when I feel I understand something in biology. I think for me it has to do with the predictability of mathematics. I feel I understand how 2 + 2 = 4, today and every time I try it. That prediction has been tested many times, and it always comes out the same. When I see the laws of nature expressed as predictable, mathematical, relationships, I get that same feeling of understanding. This is easy to see in physics, which tries to explain the forces of nature. Using the laws of physics, you can make predictions based on mathematical relationships. You can tell the velocity of Newton's apple when it hits the ground, or the amount of electricity produced by a nuclear power plant. When I consider the nature of matter, in chemistry, I see that the structure and behavior of atoms and molecules obey these same laws of physics, and they also lend themselves to mathematical predictability, and so I feel I understand chemistry, and how it works. Now modern biology, that is biology as it has come to be understood over the last 50 years or so, has made a third connection: to a great extent modern biology explains how living things function, how they do the unique things that they do, in terms of chemistry. Thus I feel the connection from biology to chemistry to physics and to mathematics that satisfies me, and that gives me the idea that I understand it.

Hierarchy among the sciences, one builds upon the other
It follows that there is a hierarchy in the sciences: a mathematician doesn't need to understand physics to do his or her work, and the physicist doesn' t have to understand chemistry, etc. Biology is the lowest on this totem pole, so the biologist has to know all these other subject; maybe that makes it highest on the totem pole, actually.

One of the main things we are going to do this semester is to explain how living things function at the level of chemistry. We will cover biochemistry, genetics, molecular biology (kind of a combination of biochemistry and genetics) and evolution. We will bring in other topics such as cell biology, but this and other basic areas of biology will be mainly left to the next semester.

Having put all this emphasis on biochemistry, let me pull back a bit and reassure you that we will not be going deeply into chemical mechanisms. This is not a course in chemistry, and although there is a prerequisite of one year of college chemistry, actually a strong high school course would also be OK. But we will be using the language of chemistry, discussing biological material as chemical structures, not just English words. We will deal extensively with organic chemicals, but organic chemistry is not necessary. Most of the special chemistry you need to know will be described as we go along.

::Characteristics of living things::
So let's get started in learning the chemistry of living things. But first we should define what we mean (that is, what I mean) by living things. My definition is fairly short, consisting of 3 properties:

Complex structure
Structure, complex structure: rock/brain; real palm tree/plastic palm tree: ~20,000 different molecules vs. ~4.

Chemical interaction with the environment.
Metabolism: living things chemically interact with the environment (breathing, eating, and excreting).

Exact reproduction of a complex interactive structure
Reproduction: this complex metabolizing structure is capable of reproducing itself, pretty nearly exactly. goat --> more goats; dandelion --> more dandelions; athlete's foot --> more athlete's foot.

In this course we will emphasize a common denominator approach; we will focus on unifying principles rather than on characteristics that distinguish one living thing from another. The latter is often used to good effect in for example,… ecology ... evolution (Darwin examined finches - he looked for the differences that set each species apart). It turns out that the common denominator approach works very well because, amazingly, we living things all do these three things (maintain a complex structure, chemically interact with the environment, and reproduce), … basically, … chemically … , the same way. Although in theory it needn't necessarily have come out that way (elephants do it one way, dandelions do another way) life, on earth at least, has evolved using one basic biochemical strategy.

As this unity became apparent, biologists began gravitating to simpler and simpler living systems to use as models for basic processes. So let's consider, what is the simplest living system?

::Cells::
Let's use an analogy from chemistry for a moment. Consider corn syrup, a sugar with an easily distinguished property: its sweetness. One microdrop is still sweet, and if you continue to take smaller and smaller bits, you finally get to one molecule of glucose (which is what corn syrup is). Split that molecule and you no longer have glucose, you have two other molecules (not glucose any more), which are no longer very sweet. In chemistry, the basic unit, and the distinguishable units, are the molecules.

We can do a similar experiment with a complex living thing, say, a person, and ask for the smallest unit that exhibits the characteristics of living things in our short list:

Take a piece of skin of a person, put it in culture (i.e., bathed in a nutrient solution simulating "blood"). It .... grows (reproduces) … has a complex structure (if looked at under a microscope), and interacts with the culture medium chemically (nutrients are consumed, substances are excreted from the skin fragment).

The person is alive, the person's arm is alive, and even the arm skin piece is alive by the 3 criteria above.

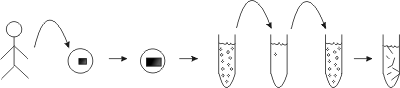
Shake the skin piece in a salt solution for a few hours; this frees up spheres (seen easily with a microscope), or cells, that make up the skin tissue. These cells also are alive: they retain the 3 characteristics we have defined, and most dramatically, they reproduce: one cell becomes many.

Now put them in a powerful blender, break them into sub-cellular pieces: Some structure still is present (but much less) and some metabolism can be measured (but much less), but there's no reproduction. These subcellualr fragments and molecuels are not living; they're dead, killed actually.

All living things are made up of cells, the basic building block in biology.
So cells are the simplest basic unit of living things, of all living things. As soon as microscopes were invented (by von Leuwenhoek in the 1700's) it became apparent that all living things were made of these cells (clams, moss, chickens). To summarize this so-called cell theory of life:

"All living things are made up of cells (or their by-products), and all cells come from other cells by growth and development."

And since a cell is alive, it represents a simple object for study, suitable for learning the most fundamental processes that characterize living things.

Let's take a quick look at this skin cell:

Some parts: 1) nucleus, 2) cytoplasm, 3) membrane (= "plasma" membrane = cell membrane)

Cytoplasmic machinery (organelles): ribosomes, mitochondria, lysosomes, etc.

The cell membrane is very important in several senses:

- Geographically, it gives definition to the cell (the cell is inside, the rest of the world outside).

- It is a barrier, but a selective one: it contains a large number of channels to allow the flow of chemicals in and out. Many of these channels have pumps associated with them. Some of these pumps pump things in, some pump things out.

- It contains sensors (mostly chemical sensors) of the environment.

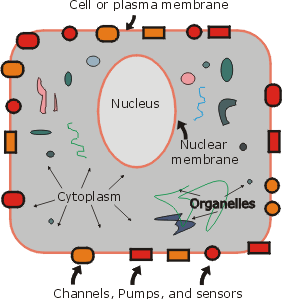Click here for a better picture of a typical animal eukaryotic cell.

[See Ch. 4 of Becker and/or Ch. 4 of Purves to read more about cell structure if you want. Most intro bio courses include this material at this point]

The size of this skin cell is about 10 µm in diameter. (µm = µ = micron = one millionth of a meter)

[As an aside, consider some units of size here: 1 millimeter (mm) = 1/25 inch (easily visualized, pinhead size); 1 micron ("micrometer", µm = 1/1000 mm, approximate the limit of a light microscope; the human eye can resolve 100 µm (0.1 mm)]

Typical animal cells = ~10 µm in diameter

The smallest cells are ~ 1 µm (~ at the limit of the light microscope, [~ the wavelength of visible light])

[ Aside : pushing to smaller length units, a nanometer = nm = 1/1,000,000 of a mm, = the size (diameter) of small molecules:

e.g., water (~0.5 nm), the alcohol ethanol (~1 nm), the sugar glucose (~1.5 nm)

[a term less used but that you may run into: the Ångstrom (A or Å)= 1/10 nm = distance between two atoms in a molecule (e.g., 2 A)]

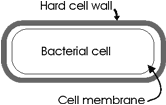
The smallest cells are ~ 1 um. What about these smallest cells, the 1 micron cells? Smaller should be simpler yet, no? There'd be less room for much stuff. This is true. The smallest cells are those of bacteria:

They are 1-2 µm in cross-section, so they are about 1/1000 the size of our 10 µm skin cell (comparing a cube of 1 um dimensions vs. a cube of 10 um dimensions).

They have a more complicated surface (there is a hard cell wall outside the plasma membrane, to protect them).

But there is no true nucleus, and much less complicated machinery inside, no big organelles. Indeed, bacteria are about the size of many animal or plant cell organelles (e.g., a mitochondrion).   Click here for a better picture of a prokaryotic cell.

The simplest living things are made up of a single cell.

A second big simplification (besides size): the skin cell was one of billions that made up the organism. For most bacteria, the number of cells in the organism is: .....   one.

That is, most bacteria are unicellular organisms.

Before we go any further considering bacteria, the simplest of all living things, let's see how they fit into a classification of all other living things according to these 2 criteria so far raised: simplicity and unicellularity.

Examples:

Some examples Unicellular Multicellular

Prokaryotes: no true bounded nucleus present
(Mostly= bacteria):
Pneumococcus (disease)
Rhizobium (plant symbiosis)
Escherichia coli (lab) Very few examples

Eukaryotes: the nucleus is a separate membrane-bound compartment
Amoebae (ponds, disease) Paramecium (ponds) Plasmodium (malaria) Yeast (beer, bread, lab) Human being
Worm (C. elegans)
Fruit fly (Drosophila)
Zebra fish
Mustard plant (Arabidopsis)
Mouse
(these examples also represent popular model organisms for research)

Click here for a view of an evolutionary classification of all living things

The simplest cell is a bacterial cell.
So the simplest living things are cells and the simplest cells appear to be bacteria. To discuss and discover most fundamental life processes, we will focus on bacteria, just as researchers did during the development of modern biology from 1950 to 1980.

Study of the basic characteristics of life in simple bacterial cells has facilitated understanding in biology.
But there are thousands of species of bacteria. How to choose ... Consider E. coli = Escherichia coli: found (by Dr. Escher) to inhabit the colon of most mammals, including people. So E. coli are readily available. They are in general non-pathogenic (most strains). They grow fast and in a very simple growth medium (just sugar and salts) in the laboratory. And some major advances in understanding genetics happened to be made by researchers studying this particular organism, starting in the 1940's. Biologists wanting to extend these initial findings did not want to complicate matters by using a different organism, so many took up E. coli as their experimental material, and so the use of this organism snowballed.

E. coli grow by binary fission. First the cell grows larger, and then when it has attained a size about double that at its smallest size, it divides into 2 cells.

Their doubling time in a simple growth medium is about 1 hour.

::What are cells made of?::
The atoms used to make a bacterial cell must be assimilated from the environment.
Here is an example of a simple, minimal, medium (the unique essential elements provided by each compound are underlined):

C₆H₁₂O₆ _{glucose, a sugar}
KH₂PO₄_{potassium phosphate}

MgSO_{4
magnesium sul}_fate

NH₄Cl _{ammonium chloride}

H₂O   water

+trace elements (e.g., Zn, Fe, Cu, Se, … )

Notice there is only one organic (= carbon (C)-containing) compound in this medium (glucose). The remaining substances are inorganic salts, providing the elements potassium, phosphorous, magnesium, sulfur, nitrogen, hydrogen and oxygen. There are also a few more metal elements needed in very small amounts.

E. coli can be made from glucose
All the carbon atoms in E. coli's 5000 types of molecules can be derived from this one molecule
Each E. coli cell contains about 10,000,000 total organic molecules, representing thousands of distinct chemical structures. So that simple diagram of binary fission means, at the least, that for one E. coli to become two E. coli, it must synthesize about 10,000,000 molecules of ~ 5000 different kinds, in just an hour, starting with just one kind of organic molecule (i.e., glucose, C₆H₁₂O₆).

We will be considering how E. coli, and some other kinds of cells, do exactly this (that is, reproduce), over the next 2 months.

I found myself explaining some of this to my father-in-law once; he had seen a diagram of the glucose molecule on my computer screen and asked what it was. I explained that it was glucose, and, with this lecture in mind, that glucose was just about all you needed to make an E. coli cell. Figuring me for a biotechnologist, and expecting ever-greater things from biology from his reading of the Tuesday Times, he said, "Are you serious? You mean you can synthesize a living E. coli cell in the laboratory from glucose? How do you do it?" When I explained: "Well, you need to start with one E. coli cell to get the second one …", his face dropped. "Oh. Okay, but that's cheating," was his reaction.

He was taking life, cell growth, for granted, because it was so familiar: children get taller and taller, the grass has to be mowed twice a week, mold the size of a quarter appears on an old peach overnight. No, we can't put together a brand new E. coli cell in a test tube; that would be a truly amazing feat. But is it really any less amazing that E. coli can do it, without a test tube? In one hour, take 10 million glucose molecules and transform them into 5000 different things, all organized to fit together in a cell that can do it all over again, in one more hour. How? How do these little cells know what to do, know how to do it, and how do they actually carry it out? If, like my father-in-law, you're not really curious about the answer, then you're probably in the wrong course.

::Cell reproduction::
How one gets two cells from one is a central problem posed in this course.

So let's get started on this 2-month explanation.

We can break the problem down into several parts, which will give you a preview of where we're headed:

To understand the question, we first must know just what molecules a cell is made of .
1. What is an E. coli cell, chemically speaking (What is it made of, what do we have to make more of?) The 5 categories of E. coli's molecules:
Polysaccharides, Lipids, Nucleic Acids, Proteins, Small molecules
A quick answer: polysaccharides, proteins, lipids, nucleic acids, and small molecules.

2. How do we get those chemicals?
Answer: From glucose, via biosynthetic chemical reactions (= metabolism).

3. Where does the energy for this process come from?
Answer: from glucose, via energy metabolism. (so glucose has a 2nd role, not just providing carbon atoms)

4. Where does E. coli get the information for doing all this?
Answer: it's hard-wired in its DNA.
-------------------------------------------------------------------------

Before we get down to business with question #1 (the chemical definition of the cell), let's consider some mathematical consequences of this reproduction by binary fission, or bacterial cell growth.

::Exponential growth::
But first, how do cells grow, in an overall view?
For example, suppose we want to measure the amount of nitrogen in a healthy viable bacterial cell. Typically, for this type of a chemical analysis, we will need several billion of these tiny cells. That's part of the simplicity of working with a unicellular organism. Since all the cells are the same, any property you measure (e.g., nitrogen content, or say, DNA content, represents a value that's true for each cell. - - That's not necessarily true if you were studying a multicellular organism, like broccoli, which is made up of many different tissues (florets, stems, leaves), with each of these tissues containing many different cell types).

Binary fission leads to exponential growth.
Say we start with one cell, put it in minimal medium, where it and its daughter cells will grow and divide once very every hour:

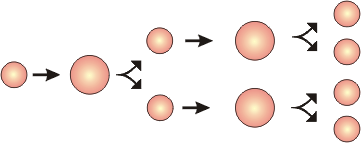
1 cell --> 2 cells in 60 min., or 1 generation; 60 min. = Doubling time = t_D

How can we calculate the time it will take to get a billion cells, so we know when to come back to the lab to collect these cells for analysis?

Let g = number of generations. From the binary fission mechanism: after 2 gens. --> 4 cells, after 3 gens. --> 8 cells, etc.

So we can see that the number of cells at any given point, N = 1 x 2^g (starting with one cell).

If we started with one million cells, then N = 10⁶ x 2^g

More generally, starting with N_o cells: N = N_o x 2^g

Since we want to know what time to come back, it is more convenient to express generations in terms of time. If we let t_D = the generation time, or doubling time, then the number of generations that have passed during the time interval t is just t/t_D. So generations, g = t/t_D.

So now N = N_o x 2^t/tD,   an equation that expresses exponential growth (with respect to time)

Or, more generally and simpler to write: N = N_o x 2^kt , where k=1/t_D,a constant for a given cell type under a defined condition (i.e., growth medium and temperature).

Exponential growth is mathematically predictable.
This exponential growth equation can be expressed in many interrelated equivalent forms, many of which are useful:

N = N_o e^kt, where k = k_e = ln2/t_D, and, writing it another way: ln(N/N_o) = k_et

and:   N = N_o10^kt, where k = k₁₀ = log2/t_D, and: log(N/N_o) = k₁₀t

Note here that the growth constant k is being defined differently for the different bases used to express the exponential nature of the growth.

The derivation of these forms is described in the exponential growth handout.
Below in italics was not in the live lecture by intention, since it is more easily followed at your leisure here. Now to return to the problem we set for ourselves, of how long it would take for one E. coli cell to grow into 1 billion cells. We could solve this equation for t, since we know we want N to be 1 billion, N_o is 1, and t_D is 1 hr. Taking the logarithm base 2 of both sides of the base 2 equation N/N_o=2^t/tD:

we get log₂ (N/N_o) = t/t_D, then, solving for t, we get t = tD[log₂(N/N_o)].

And plugging in the numbers we have: t = log₂ (1,000,000,000/1) = log₂(10⁹) hours (since the doubling time was in hour units)

But say your calculator does log base 10 but not log base 2. No problem, convert log base 2 to log base 10 (log) or to the natural log, base e (ln).

log₂ of any number X = ln_eX/ln_e2 = ln_eX/0.69 = more simply: lnX/0.69 (since "ln" with no other indicator means log base e)

or, log₂X = log₁₀X/log₁₀2 = logX/0.3 (since "log" with no other indicator means log base 10)

Applying this last one (base 10) to our problem, and since you now know that the log2 = 0.3 from the line above:

t = log₂(10⁹) = log(10⁹) /0.3 = 9/0.3 = 30. So it would take 30 hours for one cell to become one billion.

Related exponential transformations are: 2^x = 10^xlog2 and 2^x = e^xln2,

And useful numbers are: log(2) = 0.30, ln(2) = 0.69

To continue our transmogrification of these exponential growth equations:

log₂(N/N_o) = t/t_D

So log₂(N/N_o) = log(N/N_o)/log2 = t/t_D

log(N/N_o) = (log2/t_D)t = Kt, where K = log2/t_D= 0.3/t_D

or, converting back to the exponential form:

N = N_o10^Kt, where K=0.3/t_Das mentioned before.

Since most scientific calculators have natural log functions, similarly, we can write

N = N_oe^Kt, where this K = ln2/t_D = 0.69/t_D , which is the usual form of the exponential growth equation

Let's have one more look at the exponential growth equation:

We could also have approached this question of rates of change of N with time more directly and naturally using calculus. If you have a million cells, then after one generation time you will have gained 1 million. If you had 200, then you would have gained 200. In general, the rate of increase of N with time is just proportional to the number of cells you have at any moment in time, or:

dN/dt = kN

Separating variables: dN/N = kdt

Integrating between time zero when N = N_o and time t, when N = N, we get:

lnN - ln N_o = kt - 0, or ln(N/N_o) = kt, or

N = N_oe^kt, which is exactly what we derived above.

We can now calculate this constant k by considering the time interval over which N_o has doubled; in that case N/N_o = 2 and t = t_D, so 2= e^ktD. Taking the natural logarithm of both sides:

ln2=kt_D, or k=ln2/t_D, so the constant comes out exactly as before as well.

This is probably the last time you will see calculus in this course, so don't be scared off by thoughts of complex math.

You will need mostly arithmetic, some algebra, and an ability to work with exponential notation and an occasional logarithm.

There are several problems of this type in the problem book, solving for N, for t, for N_o, etc.; be sure to do them.

Finally,let's look at the growth of a bacterial culture graphically.
If we plot N vs. t :

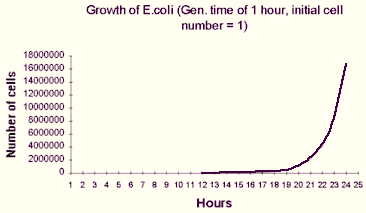
But ln(N) vs. t should give a straight line (a semi-log plot):

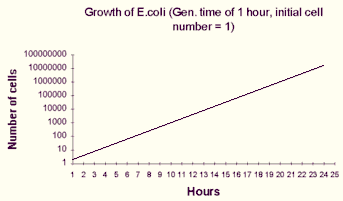
In reality, a growth curve for a bacterial culture looks more like this:

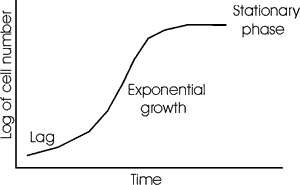
Note the 3 phases: a lag (while the cells are getting geared up), log (logarithmic) phase or exponential phase (linear on a semi-log plot such as this), and finally stationary phase (after the nutrients have been exhausted and/or toxic excreted products have built up as the culture becomes dense).So we can treat cell reproduction quantitatively, and that's what growth looks like mathematically. We now start on the problem of how the bacterium E. coli reproduces, how it grows; how we get two E. coli cells from one. First we need to know what are the chemicals that need to be made if we are to create one net E. coli cell. We need to turn to the nature of the chemicals that make up an E. coli cell, so we know what it is that we need to make in an hour.

We will start with the most abundant and most important molecule in the cell, not an organic molecule, but water, H₂O. We will use our discussion of the water molecule as a springboard for introducing different types of chemical bonds that are important in biology. Lecture 2 will start with the structure of the water molecule and how that structure determines its properties.
(C) Copyright 2001 Lawrence Chasin and Deborah Mowshowitz Department of Biological Sciences Columbia University New York, NY
Clickable pictures are from Purves, et. al., Life, 5th Edition, Sinauer-Freeman's Images of Life 5.0.
A production of the Columbia Center for New Media Teaching and Learning