Annotation category:
Chapter 1
| Note: |
Why is this the limit of human vision?
Your vision is limited by two numbers which at first seem completely unrelated to the issue: the temperature of the surface of the Sun, and the strength of gravity on the surface of the Earth. The former determines the colors, or wavelengths, of light emitted by the Sun, and the latter both sets the composition of the Earth's atmosphere (and, thus, the wavelengths of light it lets through) and the practical size of living things.
The sun-atmosphere combination leads to an abundance of light centered at a wavelength of 550 nanometers (1 nanometer = 10-9 meters) -- what we normally call "yellow" light. It is not a miraculous accident that the peak sensitivity of our eyes occurs at this same wavelength. Four hundred million years of evolution has carefully tuned out natural radiation detectors so that they are most sensitive to the wavelengths where the most light exists -- the better to see tasty morsels of food and avoid becoming such a morsel oneself. Of the 70 octaves of radiation the Universe sends our way, we "see" only one -- from about 360 nm to 720 nm. Our eyes, then, provide a sadly impoverished view of the cosmos. Our ears, at least, can hear ten octaves of sound waves -- imagine how bad Beethoven's Ninth Symphony would sound if you could only hear it one octave at a time (or, if you can't imagine it, experience it by clicking HERE
Given this narrow range of wavelength sensitivity, the other quantity that sets the limit on our ability to see small things is the size of our eyes -- or, more precisely, the diameter of the small black spot in the center of your eye through which the light enters, the pupil. Your pupil changes size somewhat, depending on the brightness of your surroundings, but the average diameter is about 0.5 cm. The smallest angle we can observe directly is given by the ratio of the wavelength of light to the diameter of the detector, or, in this case:
wavelength/diameter = 500 x 10-9 m / 5 x 10-3 m = 1 x 10-4
where the angle is measured in radians.
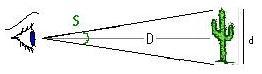
Now, the angular diameter of an object is represented as S in the following diagram:

and, for small angles (less than a few degrees), is well-approximated by the relation:
S = d/D,
or angular diameter = diameter/distance (also in radians.) The hair, held at arm's length, then, has an angular diameter of
0.1mm x (1m/103mm) / 1m = 1 x 10-4
making this just about the limit of what you can see. If you double or triple the distance, your eye can no longer see the hair at all.