Harmonic

One of an ascending series of sonic components that sound, although sometimes imperceptibly, above a clearly audible fundamental pitch.
[Example 1: violin: fundamental, and harmonics]
A harmonic is one of an ascending series of sonic components that sound, although sometimes imperceptibly, above a clearly audible fundamental pitch. When we perceive a sounding pitch, sometimes referred to as a frequency, we are perceiving a number of sonic components (higher frequencies) that combine to form the sound we are "hearing." The pitch we "hear" is called the fundamental. These higher frequencies or harmonics that sound above the fundamental make up the harmonic spectrum of a sound, and this determines the timbre or tone color of the sound. Harmonics can be difficult to perceive distinctly as single components, nevertheless they are there.
Harmonic Spectrum
There are a number of terms used to describe the frequencies of a harmonic spectrum, such as overtones or partials (see below). Moreover, we differentiate between harmonic and inharmonic frequencies that combine to form a harmonic spectrum.
Inharmonic frequencies refer to the "mistuned" sounds that are present in all sound, including musical sounds; they can be heard, for example, in the sound of the "attack" as a flute-player begins blowing a note [Ex. 2], or the metallic clanging sound as a bell is struck [Ex. 3].
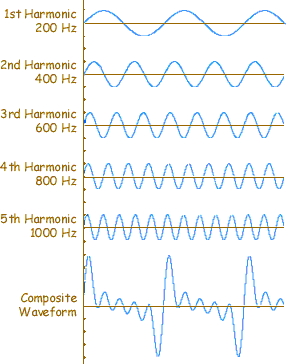
Harmonic frequencies are exact whole-number multiples of the fundamental: The first harmonic (1*1=1) is the fundamental; the second harmonic (1*2=2) sounds at twice the frequency of the fundamental; the third harmonic sounds at three times the frequency of the fundamental, and so on. The diagram below breaks down a harmonic spectrum of a sound with five harmonics. The composite waveform or the sum of all the harmonics is shown last. The sounds you will hear are sine waves. Sine waves are pure sounds or "signals," in this case computer-generated, whose harmonic spectrum contains only one component frequency -- that of the fundamental.
|
|
|
Fig 1: sine waves and composite form.
|
Overtone is a term almost synonymous with harmonic. It refers to the spectral components above the fundamental -- that is, not counting the fundamental itself. Like overtone, partials also refers to the components of the harmonic spectrum. However, partials may or may not bear a harmonic relationship to the fundamental. Strictly speaking, the first partial is in fact the fundamental.
Harmonics and the Timbres of Instruments
All musical instruments produce a unique harmonic spectrum, rather like the way fingerprints are unique. A clarinet's harmonic spectrum [Ex. 5] is different from that of a flute [Ex. 6]. Furthermore, the harmonic spectrum of a clarinet, for example, will change dynamically from note to note depending on the register and how loudly the instrument is being played. However, despite these variables, the harmonic spectrum of a clarinet, as with all instruments, has a characteristic form. In the harmonic spectrum of the clarinet, it is the odd harmonics that predominate (i.e. partials 1, 3, 5, etc.) -- they have a greater amplitude (roughly equivalent to "loudness") than the even harmonics. It is this unique combination of harmonics that produces the characteristic timbre of the clarinet.
In theory, any sound can be synthesized by computer if the frequencies of the spectral components and their relative amplitudes are known. The French composer and researcher, Jean-Claude Risset, uses a technique called "additive synthesis" to produce realistic instrumental sounds. Generally, in additive synthesis each spectral component is synthesized by a single sine wave. Figure 1 and Example 4 gave a simple example of additive synthesis. The following example is based on Risset's design to produce bell-like sounds: it uses exactly the same computer synthesis technique as Example 4.
[Example 7: Risset's bell: computer-generated additive synthesis]
There are many examples of roles that harmonics play in music and most importantly in the construction of musical instruments themselves. The bugle is a brass instrument that consists of a coiled brass tube. It does not have valves like a trumpet nor a slide like a trombone. The bugle can play essentially only one pitch -- but simple tunes are possible by sounding the harmonics of this fundamental pitch.
Harmonics are often said to have a "silvery" sound quality to them. This is partly because spectral components, which include harmonics, have a much lower amplitude or "loudness" than the fundamental. When a violin player draws the bow across the string, we can clearly hear the fundamental or the "pitch" of the string. If, however, the player touches the string very lightly in certain places called "nodes," the individual harmonics can be isolated and heard as separate components. They have soft and clear tone. In the following example, the undivided string is heard first, followed by the third, fourth, and fifth harmonics.
[Example 9: -- violin: fundamental, and harmonics]
Another way to hear violin harmonics is to slide the finger lightly up and down the string while drawing the bow -- the harmonics will "sound out" as distinct tones. Tones produced this way -- by touching nodes or by sliding --are also referred to as "natural harmonics." Natural harmonics are produced by touching a vibrating string at a place where it is divided into a whole number. (The definition octave discusses vibrating strings further.) Here, harmonics are produced by sliding the finger lightly up and down the string of a violin.
[Example 10: violin: ascending and descending harmonics]
Harmonics can be "reinforced," so as to be heard more clearly. The singing voice is particularly adept at doing this. Harmonics are created by the manipulation of vowel sounds in the mouth and throat. Here, a singer produces first a low fundamental, and then a series of harmonics over that fundamental, upward and downward. The harmonics produced most clearly here are the sixth, seventh, eighth, ninth, tenth, and twelfth.
[Example 11: harmonic singing]
All of these sounds really are produced by one singer! Harmonic singing is cultivated in certain Asian traditions, notably in Tibet and in the Tuva region of Mongolia.
Summary:
- A harmonic is one of a series of sonic components of a sound.
- A sounding pitch comprises a fundamental, and a number of harmonics above that fundamental, the totality being called a harmonic spectrum.
- The make-up of a spectrum (which harmonics are present, and in what proportion) produces the timbre, or tone color, of an instrument or voice.
- A harmonic spectrum contains both harmonic and inharmonic components.
- A timbre can be artificially synthesized by adding together sine waves.
- Harmonics can be produced separately on an instrument.
- Special vocal techniques exist for making harmonics audible in the voice.
|
Harmonic written by: Matthew Suttor
Recording & Mixing: Terry Pender, Douglas Geers Narration: Thomas Payne Producers: Ian Bent, Maurice Matiz |